Background
In the field of robotics, motion planning can be divided into two forms: freespace planning, which finds a collision free path between two points, and process planning, which governs the movement of the robot through its useful operations. Largescale robotics applications, like mobile robotics and gantry systems, have been constrained by the memory requirements of process planning. Expanding open-source software, this targeted IR&D sought to apply freespace motion planning algorithms to high degree-of-freedom process planning to quickly find practical, “good enough” process paths.
Approach
The project was broken down into two major phases. Initially, the Robot Operating System Industrial (ROS-I) process planning package Descartes_light was expanded to support dynamic graph construction algorithms. A critical addition from this phase was depth-first graph searching, which enabled significant time and memory savings by not exploring the entire graph. Secondly, an interface was created to call an existing freespace planning library, Open Motion Planning Library (OMPL), within the search methods of Descartes_light. The primary goal of calling OMPL was leveraging Rapidly Exploring Random Trees, or RRT, methods.
Accomplishments
The new approach to process planning yielded promising results. Methods developed in the first phase were designed to be run repeatedly until a desired cost or time threshold was met. A single run of a Depth-first search requires 97% less memory and runs 99% faster than the previous Descartes_light implementation. From the second phase, The RRT approach was 70% faster for mid-sized problems than traditional methods and used 98% less memory, while RRTConnect, a parallel implementation, was 85% faster, scaled to large problems, and used 98% less memory.
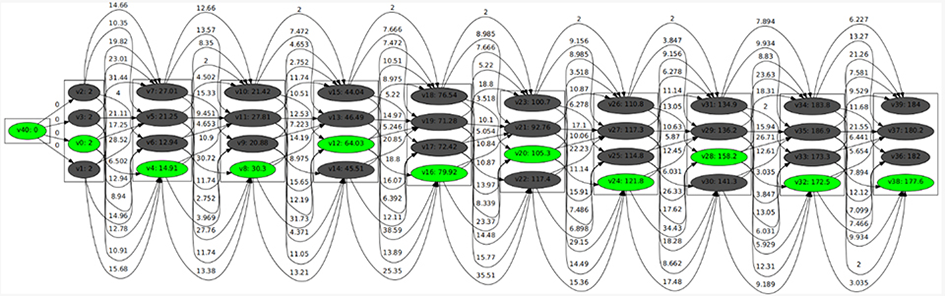
Figure 1: An example search through the motion planning ladder graph.
