Background
Machine learning (ML) methods are used to model complex patterns of behavior in applications where physics-based approaches are computationally intractable or are not feasible because the physics is not fully understood. However, ML models often take large amounts of data to train and cannot be applied outside of the training data space. Physics-informed ML is an emerging class of ML approaches that has the ability to make ML models more generalizable by “informing” the ML algorithm with basic knowledge about the physical system (e.g. constraints, governing equations, boundary conditions). This SwRI IR&D project developed a novel physics-informed ML framework that incorporates governing partial differential equations (PDEs) into the ML loss function to facilitate rapid, physically realistic predictions of stress and strain in a material body with damage. Using physics-informed ML for modeling material damage produced more physically realistic predictions than traditional ML approaches and subsequently improved predictive capability. A key outcome of this research is the significant reduction in training data requirements compared to traditional ML models, which could reduce a considerable hurdle to using data-driven models in materials engineering where material experimental data is often limited.
Approach
The physics-informed ML framework developed in this project used algorithmic differentiation to incorporate the governing solid mechanics PDEs (i.e., strain-displacement compatibility, stress equilibrium, and the stress-strain constitutive relationship) as additional constraints in the loss function of a convolutional neural network algorithm. Thus, the ML algorithm seeks to minimize the physics losses during training, along with traditional ML losses such as mean squared error (MSE) as used in this program. Convolutional neural networks are state-of-the-art ML architectures for image processing that learn patterns from the information stored in the pixels of an image. This novel Physics-Informed General Convolutional Network (PIGCN) features (1) the fusion of a dense edge network with a convolutional neural network (CNN) for specifying and enforcing boundary conditions and geometry information, (2) a data augmentation approach for learning more information from a static dataset that significantly reduces the necessary data for training, and (3) the use of a CNN for physics-informed ML applications, which is not as well explored as graph networks in the current literature.
Accomplishments
In this program, the stress equilibrium equation, strain-displacement compatibility, stress-strain constitutive relationship, and displacement and traction boundary conditions were implemented in the PIGCN loss function, along with a pixel connectivity equation that penalized pixels with physically unrealistic deformations relative to their neighbor pixels. In general, the physics losses converged faster and often to a lower loss value with PIGCN than with traditional ML approaches. PIGCN showed good predictive capability for two-dimensional plates with holes and elliptical defects, and achieved a mean average R2 value of 0.87 across all eight predictive fields of stresses, strains, and displacements (Sxx, Syy, Sxy, exx, eyy, exy, ux, and uy). Figure 1 shows an example of stress, strain, and displacement predictions made with PIGCN compared to finite element analysis results (labels) for a two-dimensional rectangular plate with an elliptical defect. The results qualitatively show good agreement between the PIGCN predictions and the labels.
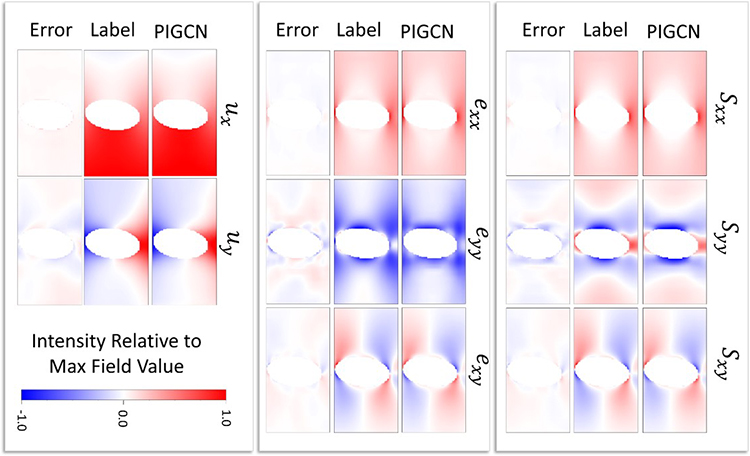
Figure 1: PIGCN predictions compared to finite element analysis results (labels) for a representative test case with an elliptical defect.
The physics-informed ML approach was also evaluated by determining the training data reduction possible with PIGCN compared to traditional ML. Figure 2 shows a comparison of the mean average R2 values achieved when training PIGCN and modified U-Net models (traditional ML models) on a random sample of 1% to 9% of the training dataset (Ntrain=1216). The mean average R2 value for PIGCN predictions (0.87) is noticeably higher than the mean average R2 value for the modified U-Net (0.72). Additionally, the mean average R2 value for PIGCN appears to converge to the full dataset average R2 value around roughly 2% of the training data (approximately 24 examples), whereas the traditional ML model does not converge with as much as 9% of the training data (approximately 108 examples). It should be noted that this outcome is dependent on the random subsets of the data selected for training, but nonetheless, is a very promising result that demonstrates the power of both the boundary encoder and the inclusion of physics-informed losses.

Figure 2: Comparison of PIGCN predictive capability to a traditional ML approach (modified U-Net architecture). The blue dashed line shows the mean average R2 value achieved by PIGCN for the entire training dataset, the green dashed line shows the mean average R2 value achieved by the traditional ML approach for the same training dataset, the blue solid line shows the mean average R2 value for PIGCN predictions as a function of the percent of the training dataset used, and the green solid line shows the mean average R2 value for the traditional ML approach as a function of the percent of the training data used.
Further development of PIGCN could result in additional reductions in training data requirements. Also, this methodology should be easily extensible to three-dimensions by replacing the two-dimensional convolutional layers with three-dimensional convolutional layers. Finally, a high priority for future research is to understand the predictive capability of this approach for more challenging materials engineering problems and identify real-world applications that this approach could support.
